Bezier Curves

The Bezier curve routines offer a very different kind of curve control where the data supplied represents control points rather than points on the curve itself.

This can be illustrated by looking at a simple Bezier curve of degree four (cubic). As  can be seen in the figure below, for each of the three Bezier curves, the points 2 & 3 deviate the line between the end points 1 and 4. Looking at the vectors between these points, the greater the magnitude, the bigger the deviation whilst their direction determines the tangent of the curve at the end points. Therefore, with the three cases below, as all the vectors between the end points and their adjacent control points are the same, the tangents at points A1, B1 and C1 are the same as are the tangents at the points A4, B4 and C4. This feature of Bezier curves is important when considering the joining of two such curves (see below).

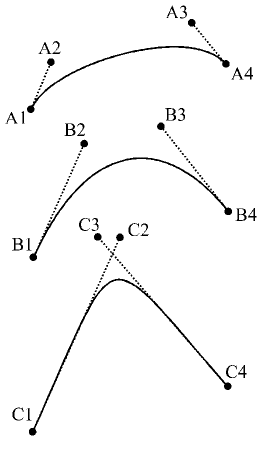Bezier Control Points

Two routines are provided to generate this type of curve in 2D:

As with the previous curve drawing routines, points2 is an array of type GPOINT and npts are the number of control points stored in the array.

Supplying a set of 6 control points (displayed as asterisks) the following curve will be drawn. Note that the curve always starts at the first control point and ends at the last control point, but in all probability will not pass through any other supplied control point.

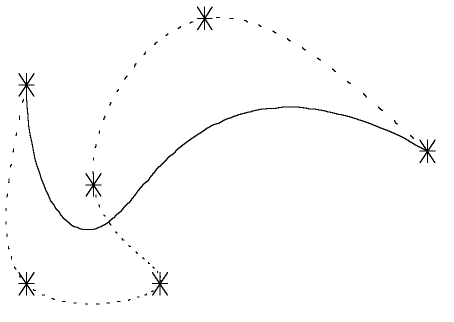Bezier Curve

End Conditions

There is no direct control over end conditions with Bezier curves, but the fact that the position of the control point adjacent to the first (or last) data point determines the tangent of the curve at that point (see above), curves can be smoothly joined by taking account of this feature.

Therefore to join two Bezier curves, the joining point must obviously be at the same coordinate position, and the distance and angle between the adjacent control points must also be the same, such that these two control points lie in a straight line. Thus in the figure below, points A4 and B1 must be the same and points A3 and B2 must form a line that intersects A4 and B1. This will give a seamless join and forms a piecewise Bezier curve.

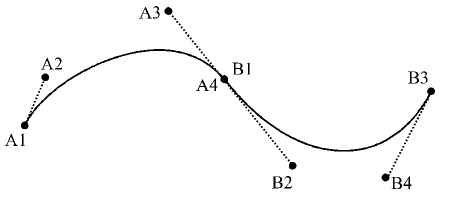Joining two Bezier Curves

Elevation and Reduction

Bezier curve drawing routines are most useful for interactive curve design where the control points can be manipulated to produce the desired shape of curve. Tighter curves can be produced where a greater number of control points are clustered. To assist in the design of appropriate curves, two auxiliary routines are also provided to increase and/or reduce the number of control points in a Bezier curve definition.

Both routines only operate on absolute coordinates and the first of them takes a set of control points as input and returns a new set with one more control point than was input, but which represents the same curve. Users must ensure that the points array is large enough to hold the additional point on return.

The second routine takes a set of control points and returns a new set with one less control point. Users should be aware that reducing the number of control points does not guarantee that the shape of the curve is maintained, but it will always be a close approximation.